COVID-19 東京都の感染者数プロファイルの解析 ［7月22日］

COVID-19 東京都の感染者数プロファイルの解析

［7月22日］

Profile analyses of COVID-19 affected numbers in Tokyo [July 22, 2020]

東京都が本日7月22日に発表した感染者数は238名でした。確定日別のデータは21日が187名です。20日分は205(33名追加)名に，19日分は137(+12名)名に増え，過去に遡って感染者数の更新がありました。

先週の水曜日発表の感染者数は165名でしたので，まだまだ増え続けています。木曜日から土曜日は発表される数が多いのですが，休日を挟むのでどのような数になるでしょうか。

このブログで報告しているデータは，検査により陽性であることを医師が確認した日別の"確定日別"のものです。実際に感染してから医師の確認までは，7日間程度の時差（4月の頃よりも短くなった）があるものと考えられ，グラフの日付を前に7日間程度移すと感染日の様子を知ることができます(図1)。

先週の16日頃は感染者数が増えたのにも拘らず，"τ×平均2"は"τ×増加率"よりも値が小さくなっています。"τ×増加率"が初めの頃の半分の0.27に近い日付が変曲点（日別感染者数のピーク）となります。計算される変曲点の日付が早まりつつあるので，実際に感染する"感染ピーク"は来週の初めと考えたほうが良さそうです。自分達の身を守るためにも，皆さんはどのように考えて行動しますか？
　

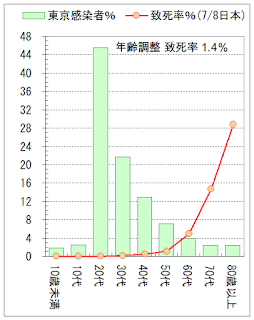Fig. 2. 年齢階級別の感染者数

東京都の最近の感染者は20代が多くを占めています。図2に7月14日から20日までの年齢階級別の感染者数（％）を示します。大多数が20代から40代です。

東京都の致死率は5月末には5.8％もありました。その後は下がり続け，7月13日には4％，本日は3.3％まで下がりました。

図2の感染者の年齢割合に，7月8日の年齢階級別の致死率を乗じて全感染者に対する致死率を算出すると，1.4％になります。この値は，台湾やオーストラリアなどの致死率の低い国々に匹敵する低さです。

致死率1.4％で第2波が経過するとしても，第2波の感染者数が1万5千名ならば，死亡者数は210名となります。50代以上の感染者が最近増えつつあるとの指摘があり，そうならば致死率は高くなります。感染しないように，罹患率を下げることが肝要です。

｢グラフの見方｣は図の下方に挙げてあります。
　

Fig. 1. 7月22日発表の東京都の確定日別データ（7月21日まで）に基づいています [クリックで拡大]

計算，理論，説明などは，7月2日分（7月3日にアップ）をご覧ください。

"τ×平均2"が，"τ×増加率"よりも小さい（下方の）時は収束の傾向（実効再生産数が減少），大きい（上方の）時はいっそう拡大の傾向（実効再生産数が増大）を意味しています。なお，"τ×増加率"自体も日々のデータに応じた最適化により，更新されていることにご注意ください。

グラフの見方

感染確定日データの日別の感染者数の累計が，"累計obs"です。ただし，最新の値で割って，最大値が1となるようにした"累計obs'"をグラフにプロットしています。

累計obsに合致するようにロジスティック関数を最適化し，最適化した関数による計算値が"累計calc"です。この値を最新の累計obsで割った"累計obs'"と"累計calc'"をプロットしています。最新の"累計obs'"は1です。

"日別obs"は，日別の感染者数です。最適化した関数から計算される日別の感染者数が"日別calc"です。

最適化した関数から計算される内的自然増加率 r から計算される実効再生産数が，"τ×増加率"です。ここでの τ (tau) は，感染者が感染させてしまう平均日数で，値は7を採用しています。初期の頃の"τ×増加率"に１を加えた数が基本再生産数に対応すると考えられ，東京都の第1波では2，第2波では1.55程度です。

日別の感染者数から見積もることができる"τ×増加率"に相当する値について，素のデータが曜日ごとのばらつきが大きいため，7日間の移動平均をとった値が"τ×平均"です。第1波について"τ×平均1"，第2波について"τ×平均2"としています。最新の3日間では7日間移動平均が適用できませんが，動向を把握するために，最新日は実際の値そのもの，前日では3日間の，前々日では5日間の移動平均を採用しています。そのため，最新日と前日の値の変動の幅は大きくなっています。

これら"τ×平均"は関数モデルが妥当ならば，"τ×増加率"に次第に合致するはずです。"τ×平均1"は第1波の"τ×増加率"によく沿っていて，"τ×平均2"は変化しながらも第2波の"τ×増加率"に追随しています。

"累計calc'"，"日別calc"と"τ×増加率"は日付を指定すれば計算できるので，数日後の値もプロットしています。

日別感染者数がピークに達するとき，"日別calc"と"τ×増加率"は変曲点に来ます。変曲点に来ると"τ×増加率"が初めのころの値の1/2となります。"τ×増加率"と"τ×平均"が次第に小さくなって，半分となる時期が感染のピークです。このときの累計感染者数を2倍すると，最大値になります。

"日別calc"はピークを挟んでグラフでは左右対称となります（偶関数です）。ピークの前と後では日別感染者数，および，その累計値（こちらは奇関数）はほとんど同じ値になります。